JDK 中提供了很多数据结构,如下所示
Collection
├ List
│ ├ LinkedList
│ ├ ArrayList
│ └ Vector
│ └Stack
└ SetMap
├ Hashtable
├ HashMap
└ WeakHashMap
Stack
public class MyStack<T> { |
Queue
public class MyQueue<T> { |
BinaryTree
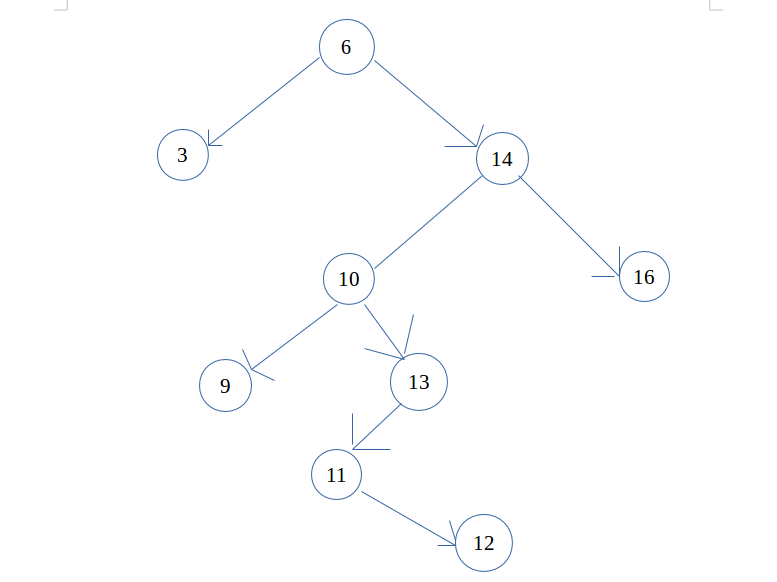
public class MyBinaryTree<T> { |
HashMap
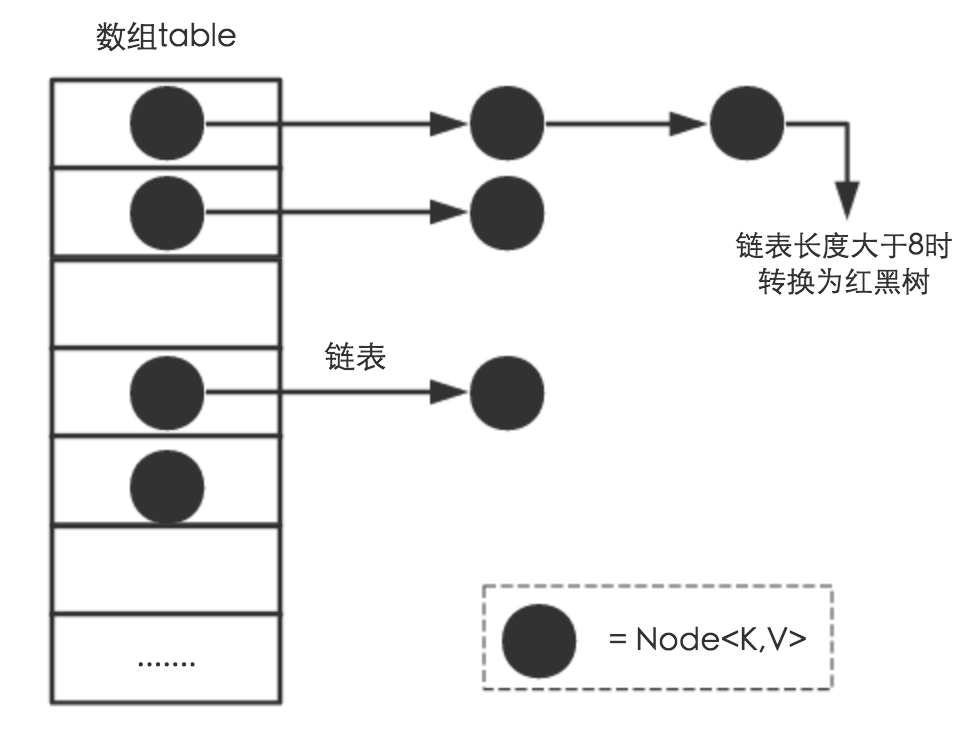
JDK 中提供了很多数据结构,如下所示
Collection
├ List
│ ├ LinkedList
│ ├ ArrayList
│ └ Vector
│ └Stack
└ SetMap
├ Hashtable
├ HashMap
└ WeakHashMap
public class MyStack<T> { |
public class MyQueue<T> { |

public class MyBinaryTree<T> { |
